TOPOLOGIE - Topologie générale

TOPOLOGIE - Topologie générale

Les notions de continuité et de limite ont une origine intuitive et l’on se propose d’analyser ici cette intuition. Considérons, par exemple, la description de la tangente T à une courbe (fig. 1) telle qu’on la trouve dans les manuels classiques de géométrie élémentaire: Si M varie sur 臨, la corde M⁰M varie continûment et, si M tend vers M⁰, la corde M⁰M a une position limite qui est T.

En disant que M⁰M varie continûment, on exprime que, si M s’approche indéfiniment d’un point M¹, la droite M⁰M s’approche indéfiniment de la droite M⁰M¹; en disant que M⁰M a une position limite T, on exprime que, si M s’approche indéfiniment de M⁰, la droite M⁰M s’approche indéfiniment de T. On peut donc donner les définitions suivantes:

– L’application f de X dans Y est continue en x ¹ si une condition suffisante pour que f (x ) soit voisin de f (x ¹) est que x soit assez voisin de x ¹;

– L’application f de X – x ⁰ dans Y a une limite y ⁰ en x ⁰, si une condition suffisante pour que f (x ) soit voisin de y ⁰ est que x soit assez voisin de x ⁰.

Pour que ces définitions deviennent des définitions mathématiques, il faut donner un sens précis aux termes «f (x ) voisin de f (x ¹) (ou de y ⁰)» et «x assez voisin de x ¹ (ou de x ⁰)». Dans les chapitres 1 et 2, on s’occupera d’abord de définir cette notion de voisinage , puis on donnera les principales propriétés des fonctions continues et des limites. Les chapitres 3 et 4 seront consacrés à l’étude de deux classes d’espaces topologiques très importantes, les espaces compacts et les espaces connexes .

La notion d’espace topologique contient en particulier celle d’espace métrique (cf. espaces MÉTRIQUES) dont l’étude est une excellente introduction à la topologie générale.

1. Espaces topologiques

Voisinages et continuité

On a vu que, pour définir les notions de limite et de continuité, on devait donner un moyen de savoir si deux points sont voisins (resp. assez voisins). Pour cela, il est assez naturel de mesurer la distance de ces deux points. On peut donc parler de continuité ou de limites pour les applications de X dans Y, si l’on a défini la distance entre les points de X et la distance entre les points de Y, c’est-à-dire si X et Y sont des espaces métriques (cf. : espaces MÉTRIQUES).

Ce point de vue est suffisant tant que X et Y sont R, R^p , les surfaces de R³, etc., et, plus généralement, pour tous les problèmes géométriques. C’est l’analyse qui a mis ses lacunes en évidence; il arrive, en effet, que l’on dispose d’applications de R^p dans un ensemble de fonctions E qui, pour des raisons propres au problème à résoudre, doivent être considérées comme continues, mais qu’il n’existe aucune métrique sur E qui les rende continues. Il faut donc donner un moyen, autre que la distance, pour savoir si deux éléments a et b de E sont voisins.

Pour cela, on se donne une famille face=F9796 Va de sous-ensembles de E que l’on appelle les voisinages de a dans E; pour dire «comment b est voisin de a », on dit dans quel voisinage de a il se trouve. Si, pour tout élément a de E, on a défini les voisinages de a dans E, on dit que E est un espace topologique ; les éléments de E sont alors appelés des points . Si E et F sont deux espaces topologiques et si f est une application de E dans F, on dit que f est continue au point a de E si: Pour tout voisinage V de f (a ) dans F, il existe un voisinage W de a dans E tel que, pour tout point b de W, le point f (b ) soit dans V. On dit que f est continue si elle est continue en chaque point de E. Tout espace métrique X devient naturellement un espace topologique si l’on choisit pour voisinages d’un point x les sous-ensembles de X qui contiennent une boule de centre x et de rayon strictement positif. On vérifie alors que, si X et Y sont métriques, pour une application f de X dans Y les deux définitions de la continuité que l’on a données coïncident.

On impose aux voisinages de vérifier les quatre conditions suivantes:

(V¹) Tout voisinage de a contient a ;

(V²) Tout sous-ensemble de l’espace E qui contient un voisinage de a est un voisinage de a ;

(V³) L’intersection d’un nombre fini de voisinages de a est un voisinage de a ;

(V⁴) Pour tout voisinage V de a , il existe un voisinage W de a tel que V soit voisinage de chacun des points de W.

Ces conditions permettent d’étendre au cas des espaces topologiques les principales propriétés des fonctions continues de R dans R. En particulier, toute somme, tout produit et tout quotient de fonctions numériques continues sont encore des fonctions numériques continues. On démontre aussi que la composée de deux applications continues est une application continue.

Ouverts et fermés

On dit qu’un sous-ensemble U de l’espace topologique E est ouvert s’il est voisinage de chacun de ses points. Les ouverts d’un espace topologique E vérifient les trois propriétés suivantes:

(O¹) L’ensemble E et l’ensemble vide sont ouverts;

(O²) Toute réunion d’ouverts est un ouvert;

(O³) Toute intersection d’un nombre fini d’ouverts est un ouvert.

La structure topologique d’un espace est déterminée par la connaissance de ses ouverts; en effet, les voisinages d’un point a de E sont les sous-ensembles de E qui contiennent un ouvert qui contient a .

Il est clair que la donnée des ouverts de E est équivalente à celle des sous-ensembles de E dont le complémentaire dans E est ouvert; ces sous-ensembles sont appelés les fermés de E; ils vérifient les trois conditions suivantes:

(F¹) L’ensemble E et l’ensemble vide sont fermés;

(F²) Toute intersection de fermés est un fermé ;

(F³) Toute réunion d’un nombre fini de fermés est un fermé.

Soit A un sous-ensemble d’un espace topologique E. D’après (O²), la réunion de tous les ouverts de E contenus dans A est un ouvert qui est évidemment le plus grand ouvert (au sens de l’inclusion) contenu dans A; on l’appelle l’intérieur de A et on le note Å. L’intérieur d’un ensemble peut être vide sans que cet ensemble le soit, comme on le voit en prenant, par exemple, pour E l’ensemble R des nombres réels muni de sa topologie usuelle, et pour A l’ensemble Q des nombres rationnels. Les ensembles ouverts sont caractérisés par le fait qu’ils sont égaux à leur intérieur.

De même, d’après (F²), l’intersection de tous les fermés contenant A est un fermé qui est le plus petit fermé contenant A: on l’appelle la fermeture ou l’adhérence de A. On vérifie facilement qu’un point x 捻 E appartient à si et seulement si, pour tout voisinage V de x , on a V 惡 A 禮; un tel point est dit adhérent à A. On dit enfin que A est partout dense dans E si = E, ce qui revient à dire que tout ouvert non vide de E rencontre A.

La considération des ouverts et des fermés donne une caractérisation très simple des applications continues. En effet, pour qu’une application f de E dans F soit continue, il faut et il suffit que, pour tout ouvert V de F, l’ensemble f ^-1(V) soit un ouvert de E; ou encore, en termes de fermés: pour tout fermé A de F, l’ensemble f ^-1(A) est fermé dans E.

Exemples

On trouvera dans de nombreux articles de mathématiques de cette encyclopédie des exemples d’ensembles munis d’une topologie. Voici quelques rappels et exemples complémentaires.

1. Sur tout ensemble X, on appelle topologie grossière la topologie dont les seuls ouverts sont X et l’ensemble vide. Tout point de X a alors un seul voisinage qui est X lui-même.

2. Il existe une topologie sur X pour laquelle tout sous-ensemble qui contient x est un voisinage de x ; c’est la topologie discrète ; tout sous-ensemble de X est alors à la fois ouvert et fermé.

3. Tout espace métrique X a une topologie naturelle (cf. espaces MÉTRIQUES). Les voisinages d’un point x sont les sous-ensembles de X, qui contiennent une boule de centre x dont le rayon est de la forme 1/n , avec n entier. Pour qu’une topologie puisse être définie par une métrique, il est donc nécessaire que tout point x possède une suite de voisinages (V^{x 1}, ..., V^{x n} , ...) telle que tout voisinage de x contienne l’un des V^{x n} ; cette remarque permet de montrer que les topologies définies aux exemples (6) et (7) ci-dessous ne peuvent pas être déduites d’une métrique.

4. Si A est un sous-ensemble de l’espace topologique E, les sous-ensembles de A de la forme A 惡 U, où U est un ouvert de E, forment les ouverts d’une topologie sur A; c’est la topologie induite sur A par la topologie de E; muni de cette topologie, A est appelé un sous-espace topologique de E.

5. Si E et F sont deux espaces topologiques, on appelle pavé ouvert de E 憐 F les sous-ensembles de la forme U 憐 V, où U est un ouvert de E et V un ouvert de F; les réunions de pavés ouverts sont les ouverts d’une topologie sur E 憐 F, appelée topologie produit . Remarquons que la topologie naturelle de R² est la topologie produit de la topologie de R par elle-même.

6. Soit E l’ensemble des applications de R dans R; pour tout nombre x et tout ouvert U de R, notons V(x , U) l’ensemble des éléments g de E tels que g (x ) appartienne à U. Parmi les topologies sur E dont les V(x , U) sont des ouverts, il en existe une qui a le moins d’ouverts; c’est la topologie de la convergence simple . Ses ouverts sont les réunions d’intersections finies d’ensembles V (x , U).

7. Soit encore E l’ensemble des applications de R dans R; pour 行 ouvert de R², notons V( 行) l’ensemble des éléments g de E tels que, pour tout x , le point (x , g (x )) soit dans 行. Les V( 行), lorsque 行 parcourt l’ensemble des ouverts de R², sont les ouverts d’une topologie sur E, que l’on appelle la topologie face=F9796 C⁰. On voit facilement qu’une application 﨏 d’un espace topologique A dans E, muni de cette topologie face=F9796 C⁰, est continue si et seulement si l’application:

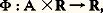qui à (a , t ) associe la valeur de 﨏(a ) en t , est continue, l’ensemble A 憐 R étant muni de la topologie produit (cf. exemple 5).

Dans les exemples 6 et 7 précédents, on a défini deux topologies distinctes sur l’ensemble E des applications de R dans R, mais il en existe bien d’autres: topologie discrète; topologie grossière; topologie de la convergence uniforme, définie par la distance:

Sur un ensemble donné, il existe ainsi beaucoup de topologies; pour certains ensembles, en particulier pour les ensembles de fonctions, plusieurs d’entre elles ont un réel intérêt; mais, sur R et sur Rⁿ , on n’utilise pratiquement que l’une d’elles, celle qui est déduite de la distance euclidienne.

Homéomorphismes

Une application f de l’espace topologique X dans l’espace topologique Y est appelée un homéomorphisme si elle est bijective et si elle est continue ainsi que son inverse.

Il est important de noter qu’une application bijective et continue n’est pas nécessairement un homéomorphisme; par exemple, si X est le sous-espace de R formé de ]a , b [ et des points a et c , avec c 礪 b , l’application f de X dans [a , b ], définie par f (t ) = t si t c et f (c ) = b , est bijective et continue, mais son inverse n’est pas continue.

Recollements de topologies

Soit (Uⁱ ), i 捻 I, une famille d’espaces topologiques, et, pour tout i , une injection 﨏ⁱ de Uⁱ dans un ensemble E. On suppose vérifiées les trois conditions suivantes:

a ) E est la réunion des images des 﨏ⁱ ;

b ) Pour tout couple (i , j ), l’ensemble 﨏^-1i ( 﨏^j (U^j )) est un ouvert de Uⁱ ;

c ) Pour tout couple (i , j ), l’application 﨏^-1j 獵 﨏ⁱ réalise un homéomorphisme de 﨏^-1i ( 﨏^j (U^j )) sur 﨏^-1j ( 﨏ⁱ (Uⁱ )) comme l’indique la figure 2.

Alors, il existe une topologie et une seule sur E, telle que, pour tout i , l’application 﨏ⁱ soit un homéomorphisme de Uⁱ sur le sous-espace 﨏ⁱ (Uⁱ ) de E. Un sous-ensemble 行 de E est ouvert pour cette topologie si et seulement si, pour tout i , 﨏^{i -1}( 行) est ouvert dans Uⁱ .

Parmi les topologies définies par ce procédé de recollement, citons la topologie de l’espace projectif réel Pⁿ (R), c’est-à-dire de l’ensemble des sous-espaces vectoriels de dimension 1 de R^{n +1}: droites de R^{n +1} passant sur l’origine. Pour tout sous-espace affine U de R^{n +1} qui ne passe pas par l’origine, on définit une injection: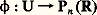

en associant à u 捻 U le sous-espace vectoriel 﨏(u ) engendré par u (fig. 3). Les conditions (a ), (b ) et (c ) sont vérifiées. Si n = 1 ou 2, l’espace Pⁿ (R) s’identifie à l’ensemble des droites du plan ou de l’espace de la géométrie élémentaire qui passent par un point M⁰ donné; c’est la topologie que nous venons de décrire qui est utilisée quand, dans la définition de la tangente, on parle de la limite d’une droite passant par M⁰ (fig. 1).

On définit de façon analogue une topologie sur l’espace projectif complexe Pⁿ (C), c’est-à-dire sur l’ensemble des sous-espaces vectoriels de dimension 1 de C^{n +1}.

2. Limites

Exemples

Dans l’analyse classique, le mot limite peut désigner des choses apparemment très diverses dont on va citer quelques exemples.

1. Limite d’une suite numérique . Soit (x ⁿ ) une suite de nombres; on dit qu’elle converge et que sa limite est y si, quel que soit le nombre strictement positif 﨎, il existe un entier N tel que, pour tout n 閭 N, on ait l’inégalité |y 漣 x ⁿ | 諒 﨎.

2. Limite uniforme d’une suite de fonctions . Soit (f ⁿ ) une suite de fonctions numériques définies sur un ensemble X; on dit qu’elle converge uniformément et que sa limite est g si, quel que soit le nombre strictement positif 﨎, il existe un entier N tel que, pour tout n 閭 N et pour tout élément z de X, on ait l’inégalité |g (z ) 漣 f ⁿ (z )| 諒 﨎.

3. Limite en + 秊 d’une fonction numérique définie sur l’intervalle [a , + 秊[. Soit f une fonction numérique définie sur l’intervalle [a , + 秊[; on dit qu’elle a une limite en + 秊 et que cette limite est le nombre y si, quel que soit le nombre strictement positif 﨎, il existe un nombre N tel que l’inégalité x 閭 sup (a , N) entraîne l’inégalité |y 漣 f (x )| 諒 﨎.

4. Limite à droite en a d’une fonction numérique définie sur ]a , b [. Soit f une fonction numérique définie sur ]a , b [; on dit que f a une limite à droite en a et que cette limite est y si, quel que soit le nombre strictement positif 﨎, il existe un nombre strictement positif 見 tel que, pour tout point x qui vérifie a 麗 x 諒 a + 見, on ait |y 漣 f (x )| 諒 﨎.

Filtres

Il existe une certaine parenté entre ces définitions; pour dégager ce qu’elles ont de commun, H. Cartan a introduit la notion de filtre. Un filtre sur l’ensemble A est, par définition, un ensemble 杻 de parties de A, qui vérifie les trois conditions suivantes:

a ) Tout élément de 杻 est non vide;

b ) L’intersection d’un nombre fini d’éléments de 杻 est un élément de 杻;

c ) Toute partie de A qui contient un élément de 杻 est elle-même un élément de 杻.

Si f est une application de A dans un espace topologique X, on dit que le point y de X est limite de f suivant le filtre 杻 si, pour tout voisinage V de y dans X, il existe un élément F de 杻 tel que f (a ) soit dans V chaque fois que a appartient à F.

Montrons que l’on a obtenu le résultat cherché, c’est-à-dire que les quatre notions de limites définies plus haut sont des cas particuliers de limite suivant un filtre.

Sur l’ensemble N des entiers naturels, les complémentaires des parties finies forment un filtre 杻^N (que l’on appelle souvent filtre de Fréchet). Dire que la suite numérique (x ⁿ ) converge et a pour limite y (exemple 1), c’est dire que y est limite de la fonction de N dans R qui à n associe x ⁿ , suivant le filtre 杻^N.

Dire que la suite de fonctions numériques (f ⁿ ) converge uniformément et qu’elle a pour limite g (exemple 2), c’est dire que, si l’on note E l’ensemble des fonctions de X dans R et si l’on munit E de la distance de la convergence uniforme, g est limite suivant le filtre 杻^N de l’application de N dans E qui à n associe f ⁿ .

Dire que y est la limite de f en + 秊 (exemple 3), c’est dire que y est la limite de f suivant le filtre 杻+ 秊 formé des complémentaires des parties majorées de [a , + 秊[.

Dire que y est la limite à droite en a de la fonction numérique f définie sur ]a , b [ (exemple 4), c’est dire que y est la limite de f suivant le filtre 杻^{a +} formé des intersections de ]a , b [ et des voisinages de a dans R.

On démontre que, si f et g sont des applications de A dans R qui ont des limites y et z suivant le filtre 杻, alors y + z (resp. yz ) est limite de f + g (resp. limite de fg ) suivant le filtre 杻.

Notons encore que, si A est un espace topologique, les voisinages d’un point a forment un filtre sur A; dire que l’application f de A dans l’espace topologique X est continue en a , c’est dire que f a pour limite f (a ) suivant ce filtre.

Séparation

Une suite numérique ne peut avoir deux limites; de même, une fonction numérique ne peut avoir deux limites en + 秊 (ou en a ). Mais, si l’ensemble A est muni du filtre 杻 et si f est une application de A dans un espace topologique X, deux points distincts de X peuvent être limites de f suivant le filtre 杻; par exemple, si X est muni de la topologie grossière, tout point de X est limite de f suivant le filtre 杻. Pour avoir l’unicité des limites pour les applications à valeurs dans X, on doit supposer que X vérifie la condition suivante: Deux points distincts de X possèdent des voisinages disjoints. On dit alors que X est séparé . Tous les espaces métriques sont séparés, à cause de la relation d (x , y ) = 0 輦 x = y ; c’est le fait que R est séparé qui permet de faire les raisonnements classiques dits «par passage à la limite» ou «par continuité».

3. Espaces compacts

Les intervalles fermés bornés de R ont des propriétés topologiques remarquables, connues depuis très longtemps; ces propriétés découlent toutes du fait qu’ils vérifient la condition suivante, appelée condition de Borel-Lebesgue (cf. le théorème (7) du chapitre 4 de l’article CALCUL INFINITÉSIMAL - CALCUL À UNE VARIABLE).

Condition (BL) . On dit que l’espace topologique E vérifie la condition de Borel-Lebesgue si, quelle que soit la famille d’ouverts (Uⁱ ), i 捻 I, de E telle que:

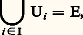il existe un sous-ensemble fini J de I tel que:

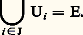Par définition, on dit qu’un espace topologique est compact s’il est séparé et s’il vérifie la condition de Borel-Lebesgue. Cette condition est équivalente à chacune des deux suivantes.

Condition (BL) . Quelle que soit la famille (Fⁱ ), i 捻 I, de fermés de E d’intersection vide , il existe un sous-ensemble fini J de I tel que l’intersection des Fⁱ , pour i 捻 J, soit vide.

Condition (BL) . Quelle que soit la famille (Fⁱ ), i 捻 I, de fermés de E, si, pour tout sous-ensemble fini J de I,

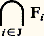est non vide, il existe (au moins) un point de E qui appartient à tous les Fⁱ .

Exemples

L’intervalle [a , b ] de R est compact. Plus généralement, un sous-espace A de R est compact si et seulement s’il est fermé et borné. De la même façon, les sous-espaces compacts de Rⁿ sont les fermés bornés. Tout sous-espace fermé d’un compact est compact. Tout produit d’espaces compacts est compact.

Propriétés

Citons les plus importantes propriétés des espaces compacts.

1. Si X est compact et Y séparé, l’image d’une application continue de X dans Y est un sous-espace compact de Y. En particulier, si A est compact, l’image d’une application continue f de A dans R est un sous-espace compact de R; c’est donc un sous-ensemble fermé borné de R; c’est pourquoi f est une application bornée et atteint ses bornes.

2. Propriété de Bolzano-Weierstrass . Soit (u ⁿ ), n 捻 N, une suite de points du compact A. Alors, il existe un point a de A tel que tout voisinage de a contienne u ⁿ pour une infinité de valeurs de n ; un tel point a est appelé une valeur d’adhérence de la suite.

La démonstration, par l’absurde, est la suivante: Si, pour tout point x de A, il existait un voisinage ouvert V^x de x qui ne contienne qu’un nombre fini des u ⁿ , alors, comme N est infini, l’ensemble A ne pourrait pas être recouvert par un nombre fini des V^x .

Réciproquement, cette propriété de Bolzano-Weierstrass entraîne la propriété de Borel-Lebesgue si l’espace considéré est un espace métrique.

3. Tout espace métrique compact est complet (cf. espaces MÉTRIQUES, chap. 3).

4. Tout sous-espace compact d’un espace topologique E est un fermé de E.

5. Toute fonction continue d’un espace compact dans un espace métrique est uniformément continue (cf. espaces MÉTRIQUES, chap. 2).

Espaces localement compacts

On dit qu’un espace métrique est localement compact s’il est séparé et si chacun de ses points possède un voisinage compact. On se convainc de l’importance des espaces localement compacts en remarquant que tous les espaces de la géométrie (R, Rⁿ , surfaces, courbes, variétés différentiables...) sont localement compacts. Tout espace localement compact est homéomorphe à un ouvert d’un espace compact. En fait, on peut même s’arranger pour que cet ouvert soit le complémentaire d’un unique point de l’espace compact (compactification d’Alexandrof).

Parmi les propriétés les plus utiles des espaces localement compacts, citons les deux suivantes, qui concernent les problèmes de prolongement de fonctions continues lorsque E est un espace localement compact «dénombrable à l’infini», c’est-à-dire tel qu’il existe une famille dénombrable (Kⁿ ), n 捻 N, de sous-espaces compacts de E, avec:

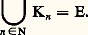1. Théorème de Tietze . Toute fonction continue d’un fermé de E dans R est la restriction d’une fonction continue définie sur E tout entier.

2. Existence de «partitions de l’unité» . Pour tout recouvrement de E par des ouverts (Uⁱ ), i 捻 I, il existe une famille de fonctions (f ⁱ ), i 捻 I, telle que:

a ) quel que soit le point x n’appartenant pas à Uⁱ , on a f ⁱ (x ) = 0,

b ) en chaque point x , il n’existe qu’un nombre fini des f ⁱ qui ne s’annulent pas,

c ) pour tout point x , on a:

une telle famille de fonctions est appelée une partition de l’unité relative au recouvrement (Uⁱ ), i 捻 I, donné.

4. Espaces connexes

En regardant une figure géométrique, chacun sait dire si elle est formée de plusieurs morceaux disjoints. La connexité est la notion mathématique qui correspond à cette réalité physique. Si la figure F est formée de deux morceaux disjoints A et B, tout point de F assez voisin de A est encore dans A, et tout point de B assez voisin de B est encore dans B. Donc A et B sont des ouverts non vides et disjoints de F. Inversement, si F est d’un seul tenant, il n’existe pas de partition de F en deux ouverts non vides disjoints. Mathématiquement, on exprime ce fait en disant que F est connexe.

Les sous-espaces connexes de R sont les intervalles de R, ouverts, semi-ouverts ou fermés, bornés ou non. Si X est connexe et si f : XY est une application continue, l’image de f est un sous-espace connexe de Y. En particulier, l’image d’une application continue f : [a , b ]R est un intervalle de R. C’est le théorème de la valeur intermédiaire , qui s’énonce comme suit.

Théorème . Si f est une application continue de [a , b ] dans R, quel que soit z compris entre f (a ) et f (b ), il existe un point c de ]a , b [ tel que f (c ) = z (cf. CALCUL INFINITÉSIMAL - Calcul à une variable, chap. 9, théorème 14 bis ).

Notons encore que, si X est connexe, toute fonction localement constante de X dans Y, c’est-à-dire telle que tout point x de X possède un voisinage sur lequel f est constante, est constante dans X tout entier. Le principe des zéros isolés pour les fonctions analytiques (cf. FONCTIONS ANALYTIQUES -Fonctions d’une variable, chap. 1) utilise ce type d’argumentation.

Encyclopédie Universelle. 2012.